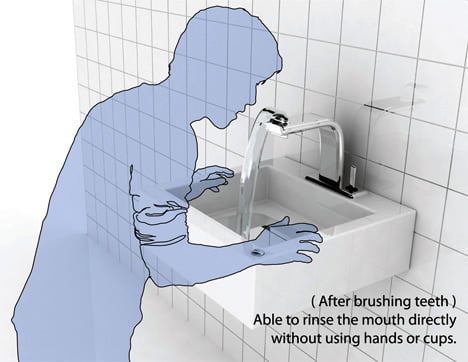
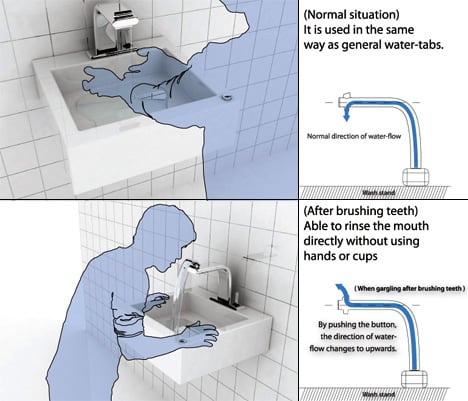
Your Morning routine: head to the sink, open the tap, water pours down, brush your teeth, and gargle with cup.
My Routine: head to the sink, open Fountain Tab, water flows upwards (with the push of a button), brush my teeth, no cups for gargling…just lap up the water directly from the faucet.
I told you so, my faucet is way too cooler than yours!
Designers: Jin-sun Park & Byungmin Woo