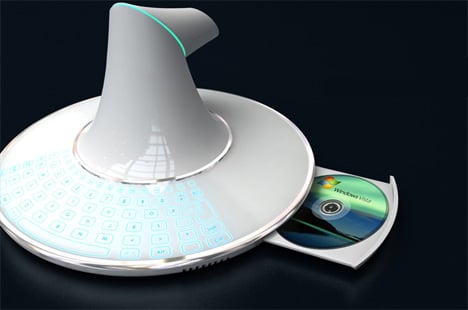
Wow, I have seen parsecs worth of concept computer designs during my visit here on Earth, but nothing like this “B-membrane” design by Korean designer Won-Seok Lee. He has taken the need for a bulky monitors right out of the equation and opted for beaming your YouTubing onto any surface you can point the omni-directional projector at. Some highlights of this Kubrick inspired mother ship computer include a membrane keyboard that appears when needed, integrated optical drive and when not used as a computer, the projector can beam ambient light effects on any surface you desire.
Designer: Won-Seok Lee




At night it can be used for mood lighting.